 Home Page
Home Page Site Map
Site Map Login/out
Login/out Message Board
Message Board Download
Download(c) 2005-2025 XLOG Technologies AG
The web site www.xlog.ch can be searched via text search by typing a search expression into the search box. A result list will be produced from which you can choose a document. The ranking of the results is detailed below.
The ranking measures the hit on the page, as well as the contribution of each other page. Is there a hit on the page, then the contribution is (1-λ)/τ, otherwise the contribution is λ/τ. This can be depicted graphically as follows:
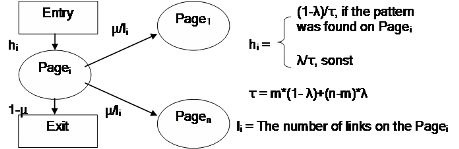
By the way that the rank includes also pages without hits, the ranking is a mix of a general weighting of the pages in the whole collection and of a weighting with respect to the pages inside the collection that match the pattern. But because the links between the pages can lead into cycles, the rank becomes a recursive matrix equation:
R = L*R + HWe solve this equation exactly in that we calculate R = (E-L)-1*H. The matrix inversion (E-L)-1 is only computed once for the web site and is stored across the pages of the web site. During each search only H is recomputed and the matrix multiplication is performed. In consequence the method behaves time quadric on queries, and not cubic.